2. Diagnostic Modeling Overview and Perspectives#
This text prescribes a formal model diagnostic approach that is a deliberative and iterative combination of state-of-the-art UC and global sensitivity analysis techniques that progresses from observed history-based fidelity evaluations to forward looking resilience and vulnerability inferences [12, 13].
2.1. Overview of model diagnostics#
Model diagnostics provide a rich basis for hypothesis testing, model innovation, and improved inferences when classifying what is controlling highly consequential results (e.g., vulnerability or resilience in coupled human-natural systems). Fig. 2.1, adapted from [6], presents idealized illustrations of the relationship between UC and global sensitivity analysis for two coupled simulation models. The figure illustrates how UC can be used to address how uncertainties in various modeling decisions (e.g., data inputs, parameters, model structures, coupling relationships) can be sampled and simulated to yield the empirical model output distribution(s) of interest. Monte Carlo frameworks allow us to sample and propagate (or integrate) the ensemble response of the model(s) of focus. The first step of any UC analysis is the specification of the initial input distributions as illustrated in Fig. 2.1. The second step is to perform the Monte Carlo simulations. The question can then be raised, which of the modeling assumptions in our Monte Carlo experiment are the most responsible for the resulting output uncertainty. We can answer this question using global sensitivity analysis as illustrated in Fig. 2.1. Global sensitivity analysis can be defined as a formal Monte Carlo sampling and analysis of modeling choices (structures, parameters, inputs) to quantify their influence on direct model outputs (or output-informed metrics). UC experiments by themselves do not explain why a particular uncertain outcome is produced, but produce distributions of model outcomes, as portrayed by the yellow curve. The pie chart shown in Fig. 2.1 is a conceptual representation of the results of using a global sensitivity analysis to identify those factors that are most dominantly influencing results, either individually or interactively [14].
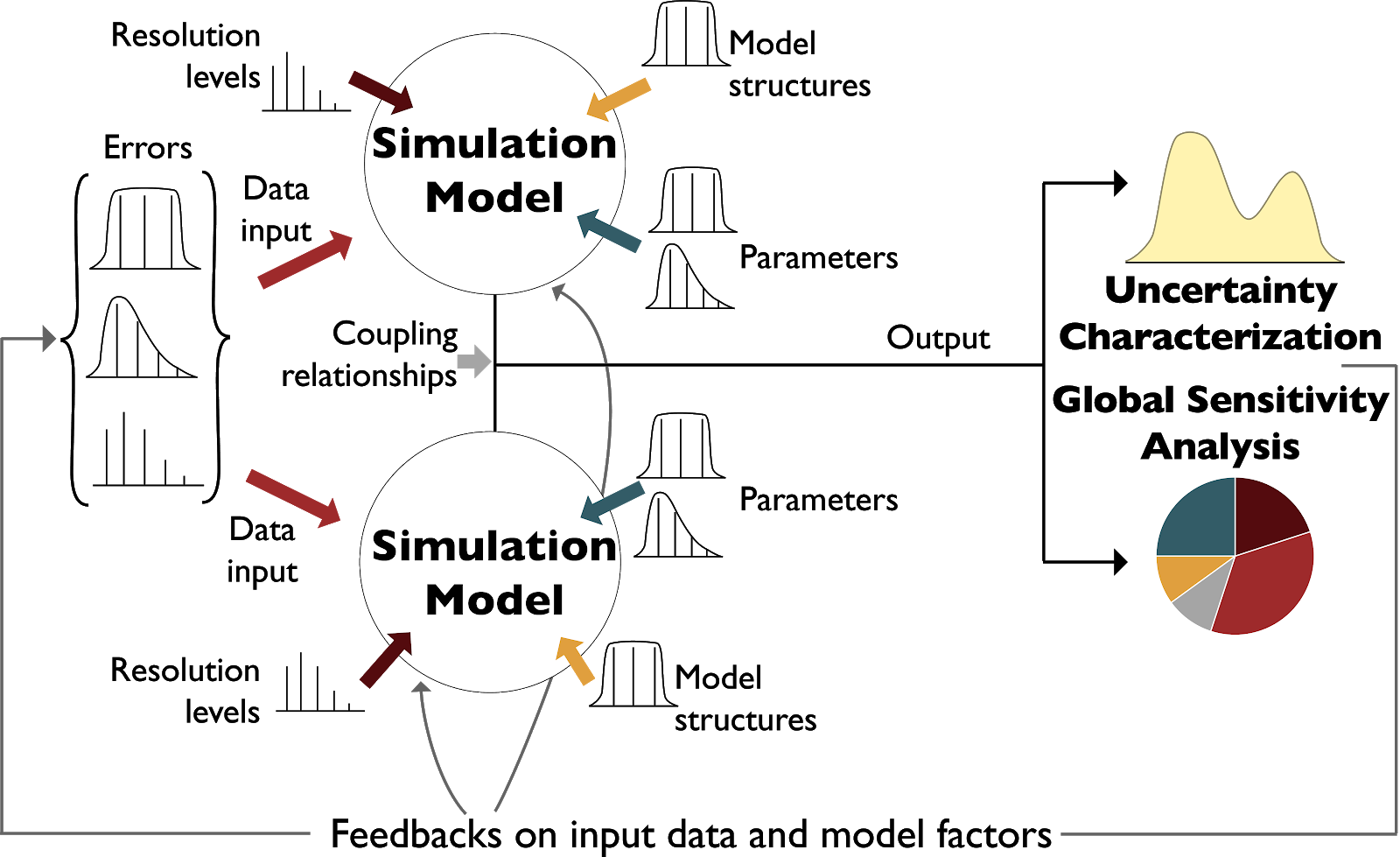
Fig. 2.1 Idealized uncertainty characterization and global sensitivity analysis for two coupled simulation models. Uncertainty coming from various sources (e.g., inputs, model structures, coupling relationships) is propagated through the coupled model(s) to generate empirical distributions of outputs of interest (uncertainty characterization). This model output uncertainty can be decomposed to its origins, by means of sensitivity analysis. Figure adapted from Saltelli et al. [6].#
UC and global sensitivity analysis are not independent modeling analyses. As illustrated here, any global sensitivity analysis requires an initial UC hypothesis in the form of statistical assumptions and representations for the modeling choices of focus (structural, parametric, and data inputs). Information from these two model diagnostic tools can then be used to inform data needs for future model runs, experiments to reduce the uncertainty present, or the simplification or enhancement of the model where necessary. Together UC and global sensitivity analysis provide a foundation for diagnostic exploratory modeling that has a consistent focus on the assumptions, structural model forms, alternative parameterizations, and input data sets that are used to characterize the behavioral space of one or more models.
2.2. Perspectives on diagnostic model evaluation#
When we judge or diagnose models, the terms “verification” and “validation” are commonly used. However, their appropriateness in the context of numerical models representing complex coupled human-natural systems is questionable [15, 16]. The core issue relates to the fact that these systems are often not fully known or perfectly implemented when modeled. Rather, they are defined within specific system framings and boundary conditions in an evolving learning process with the goal of making continual progress towards attaining higher levels of fidelity in capturing behaviors or properties of interest. Evaluating the fidelity of a model’s performance can be highly challenging. For example, the observations used to evaluate the fidelity of parameterized processes are often measured at a finer resolution than what is represented in the model, creating the challenge of how to manage their relative scales when performing evaluation. In other cases, numerical models may neglect or simplify system processes because sufficient data is not available or the physical mechanisms are not fully known. If sufficient agreement between prediction and observation is not achieved, it is challenging to know whether these types of modeling choices are the cause, or if other issues, such as deficiencies in the input parameters and/or other modeling assumptions are the true cause of errors. Even if there is high agreement between prediction and observation, the model cannot necessarily be considered validated, as it is always possible that the right values were produced for the wrong reasons. For example, low error can stem from a situation where different errors in underlying assumptions or parameters cancel each other out (“compensatory errors”). Furthermore, coupled human-natural system models are often subject to “equifinality”, a situation where multiple parameterized formulations can produce similar outputs or equally acceptable representations of the observed data. There is therefore no uniquely “true” or validated model, and the common practice of selecting “the best” deterministic calibration set is more of an assumption than a finding [17, 18]. The situation becomes even more tenuous when observational data is limited in its scope and/or quality to be insufficient to distinguish model representations or their performance differences.
These limitations on model verification undermine any purely positivist treatment of model validity: that a model should correctly and precisely represent reality to be valid. Under this perspective, closely related to empiricism, statistical tests should be used to compare the model’s output with observations and only through empirical verification can a model or theory be deemed credible. A criticism to this viewpoint (besides the aforementioned challenges for model verification) is that it reduces the justification of a model to the single criterion of predictive ability and accuracy [19]. Authors have argued that this ignores the explanatory power held in models and other procedures, which can also advance scientific knowledge [20]. These views gave rise to relativist perspectives of science, which instead place more value on model utility in terms of fitness for a specific purpose or inquiry, rather than representational accuracy and predictive ability [21]. This viewpoint appears to be most prevalent among practitioners seeking decision-relevant insights (i.e., inspire new views vs. predict future conditions). The relativist perspective argues for the use of models as heuristics that can enhance our understanding and conceptions of system behaviors or possibilities [22]. In contrast, natural sciences favor a positivist perspective, emphasizing similarity between simulation and observation even in application contexts where it is clear that projections are being made for conditions that have never been observed and the system of focus will have evolved structurally beyond the model representation being employed (e.g., decadal to centennial evolution of human-natural systems).
These differences in prevalent perspectives are mirrored in how model validation is defined by the two camps: From the relativist perspective, validation is seen as a process of incremental “confidence building” in a model as a mechanism for insight [23], whereas in natural sciences validation is framed as a way to classify a model as having an acceptable representation of physical reality [16]. Even though the relativist viewpoint does not dismiss the importance of representational accuracy, it does place it within a larger process of establishing confidence through a variety of tools. These tools, not necessarily quantitative, include communicating information between practitioners and modelers, interpreting a multitude of model outputs, and contrasting preferences and viewpoints.
On the technical side of the argument, differing views on the methodology of model validation appear as early as in the 1960’s. Naylor and Finger [24] argue that model validation should not be limited to a single metric or test of performance (e.g., a single error metric), but should rather be extended to multiple tests that reflect different aspects of a model’s structure and behavior. This and similar arguments are made in literature to this day [12, 25, 26, 27, 28] and are primarily founded on two premises. First, that even though modelers widely recognize that their models are abstractions of the truth, they still make truth claims based on traditional performance metrics that measure the divergence of their model from observation [28]. Second, that the natural systems mimicked by the models contain many processes that exhibit significant heterogeneity at various temporal and spatial scales. This heterogeneity is lost when a single performance measure is used, as a result of the inherent loss of process information occurring when transitioning from a highly dimensional and interactive system to the dimension of a single metric [15]. These arguments are further elaborated in Chapter 4.
Multiple authors have proposed that the traditional reliance on single measures of model performance should be replaced by the evaluation of several model signatures (characteristics) to identify model structural errors and achieve a sufficient assessment of model performance [12, 29, 30, 31]. There is however a point of departure here, especially when models are used to produce inferences that can inform decisions. When agencies and practitioners use models of their systems for public decisions, those models have already met sufficient conditions for credibility (e.g., acceptable representational fidelity), but may face broader tests on their salience and legitimacy in informing negotiated decisions [22, 32, 33]. This presents a new challenge to model validation, that of selecting decision-relevant performance metrics, reflective of the system’s stakeholders’ viewpoints, so that the most consequential uncertainties are identified and addressed [34]. For complex multisector models at the intersection of climatic, hydrologic, agricultural, energy, or other processes, the output space is made up of a multitude of states and variables, with very different levels of salience to the system’s stakeholders and to their goals being achieved [35]. This is further complicated when such systems are also institutionally and dynamically complex. As a result, a broader set of qualitative and quantitative performance metrics is necessary to evaluate models of such complex systems, one that embraces the plurality of value systems, agencies and perspectives present. For IM3, even though the goal is to develop better projections of future vulnerability and resilience in co-evolving human-natural systems and not to provide decision support per se, it is critical for our multisector, multiscale model evaluation processes to represent stakeholders’ adaptive decision processes credibly.
As a final point, when a model is used in a projection mode, its results are also subject to additional uncertainty, as there is no guarantee that the model’s functionality and predictive ability will stay the same as the baseline, where the verification and validation tests were conducted. This challenge requires an additional expansion of the scope of model evaluation: a broader set of uncertain conditions needs to be explored, spanning beyond historical observation and exploring a wide range of unprecedented conditions. This perspective on modeling, termed exploratory [36], views models as computational experiments that can be used to explore vast ensembles of potential scenarios to identify those with consequential effects. Exploratory modeling literature explicitly orients experiments toward stakeholder consequences and decision-relevant inferences and shifts the focus from predicting future conditions to discovering which conditions lead to undesirable or desirable consequences.
This evolution in modeling perspectives can be mirrored by the IM3 family of models in a progression from evaluating models relative to observed history to advanced formalized analyses to make inferences on multisector, multiscale vulnerabilities and resilience. Exploratory modeling approaches can help fashion experiments with large numbers of alternative hypotheses on the co-evolutionary dynamics of influences, stressors, as well as path-dependent changes in the form and function of human-natural systems [37]. The aim of this text is to therefore guide the reader through the use of sensitivity analysis (SA) methods across these perspectives on diagnostic and exploratory modeling.
Note
The following articles are suggested as fundamental reading for the information presented in this section:
Naomi Oreskes, Kristin Shrader–Frechette, and Kenneth Belitz. Verification, Validation, and Confirmation of Numerical Models in the Earth Sciences. Science, 263 (5147): 641-646, February 1994. URL: https://science.sciencemag.org/content/263/5147/641. DOI: https://doi.org/10.1126/science.263.5147.641.
Keith Beven. Towards a coherent philosophy for modelling the environment. Proceedings of the Royal Society of London. Series A: mathematical, physical and engineering sciences, 458 (2026): 2465-2484, 2002.
Eker, S., Rovenskaya, E., Obersteiner, M., Langan, S., 2018. Practice and perspectives in the validation of resource management models. Nature Communications 9, 1–10. https://doi.org/10.1038/s41467-018-07811-9
The following articles can be used as supplemental reading:
Canham, C.D., Cole, J.J., Lauenroth, W.K. (Eds.), 2003. Models in Ecosystem Science. Princeton University Press. https://doi.org/10.2307/j.ctv1dwq0tq